---
title: "Usage"
output: rmarkdown::html_vignette
vignette: >
  %\VignetteIndexEntry{Usage}
  %\VignetteEngine{knitr::rmarkdown}
  \usepackage[utf8]{inputenc}
  \usepackage{xcolor}
  \usepackage{bbding}
bibliography: "`r here::here('vignettes', 'library.bib')`"
---

```{r setup, include=FALSE, message=FALSE, warning=FALSE}
knitr::opts_chunk$set(
  collapse = TRUE,
  warning = FALSE,
  message = FALSE,
  fig.retina = 3,
  comment = "#>"
)
```

This package provides functions for designing surveys and conducting power analyses for choice-based conjoint survey experiments in R. Each function in the package begins with `cbc_` and supports a step in the following process for designing and analyzing surveys:

<center>
<img src="https://jhelvy.github.io/cbcTools/reference/figures/program_diagram.png" width=100%>
</center>

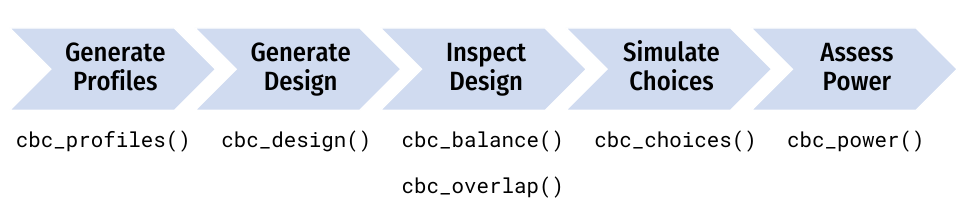This guide walks through each step of this design process.

# Generate profiles

## All profiles 

The first step in designing an experiment is to define the attributes and levels for your experiment and then generate all of the `profiles` of each possible combination of those attributes and levels. For example, let's say you're designing a conjoint experiment about apples and you want to include `price`, `type`, and `freshness` as attributes. You can obtain all of the possible profiles for these attributes using the `cbc_profiles()` function:

```{r}
library(cbcTools)

profiles <- cbc_profiles(
  price     = seq(1, 5, 0.5), # $ per pound
  type      = c('Fuji', 'Gala', 'Honeycrisp'),
  freshness = c('Poor', 'Average', 'Excellent')
)

nrow(profiles)
head(profiles)
tail(profiles)
```

## Restricted profiles 

Depending on the context of your survey, you may wish to eliminate some profiles before designing your conjoint survey (e.g., some profile combinations may be illogical or unrealistic). 

> **CAUTION: including restrictions in your designs can substantially reduce the statistical power of your design, so use them cautiously and avoid them if possible**.

If you do wish to restrict some attribute level combinations, you can do so using the `cbc_restrict()` function, which takes the full set of `profiles` along with any number of restricted pairs of attribute levels, defined as pairs of logical expressions separated by commas. In the example below, I include the following restrictions (these are arbitrary and just for illustration purposes):

- `"Gala"` apples will not be shown with the prices `1.5`, `2.5`, and `3.5`.
- `"Honeycrisp"` apples will not be shown with prices less than `2`.
- `"Fuji"` apples will not be shown with the `"Excellent"` freshness.

With these restrictions, there are now only 57 profiles compared to 81 without them:

```{r}
restricted_profiles <- cbc_restrict(
    profiles,
    type == "Gala" & price %in% c(1.5, 2.5, 3.5),
    type == "Honeycrisp" & price < 2,
    type == "Fuji" & freshness == "Excellent"
)

dim(restricted_profiles)
```

# Generate survey designs

Once a set of profiles is obtained, a conjoint survey can then be generated using the `cbc_design()` function. The function takes several arguments that are common to all design methods:

- `profiles`: A data frame of profiles (generated with `cbc_profiles()`) to use in the design (with or without restrictions).
- `n_resp`: The number of respondents in the survey.
- `n_alts`: The number of alternatives per question.
- `n_q`: The number of questions per respondent.
- `method`: The design strategy to use (defaults to `"random"`).

The `method` argument determines the design strategy to use: `"random"`, `"full"`, `"orthogonal"`, `"dopt"`, `"CEA"`, or `"Modfed"`. All methods ensure that the two following criteria are met:

1. No two profiles are the same within any one choice set.
2. No two choice sets are the same within any one respondent.

The table below summarizes method compatibility with other design options, including the ability to include a "no choice" option, the creation of a "labeled" design (also called a "alternative-specific" design), the use of restricted profiles, and the use of blocking.

Method | No choice | Labeled designs | Restricted profiles | Blocking
---|---|---|---|---
`"random"`     | Yes | Yes | Yes | No
`"full"`       | Yes | Yes | Yes | Yes
`"orthogonal"` | Yes | No  | No  | Yes
`"dopt"`       | Yes | No  | Yes | Yes
`"CEA"`        | Yes | No  | No  | Yes
`"Modfed"`     | Yes | No  | Yes | Yes

The returned `design` data frame contains a choice-based conjoint survey design where each row is an alternative. It includes the following columns:

- `profileID`: Identifies the profile in `profiles`.
- `respID`: Identifies each survey respondent.
- `qID`: Identifies the choice question answered by the respondent.
- `altID`:Identifies the alternative in any one choice observation.
- `obsID`: Identifies each unique choice observation across all respondents.
- `blockID`: If blocking is used, identifies each unique block.

## Random designs

The `"random"` method (the default) creates a design where choice sets are created by randomly sampling from the full set of `profiles` *with* replacement. This means that few (if any) respondents will see the same sets of choice sets. This method is less efficient than other approaches and may lead to a deficient experiment in smaller sample sizes, though it guarantees equal ability to estimate main and interaction effects.

```{r}
set.seed(5678)

design_random <- cbc_design(
  profiles = profiles,
  n_resp   = 900, # Number of respondents
  n_alts   = 3,   # Number of alternatives per question
  n_q      = 6,   # Number of questions per respondent
  method   = 'random' # This is the default method
)

dim(design_random)  
head(design_random) 
```

## Full factorial designs

The `"full"` method for ("full factorial") creates a design where choice sets are created by randomly sampling from the full set of `profiles` *without replacement*. The choice sets are then repeated to meet the desired number of survey respondents (determined by `n_resp`). If blocking is used, choice set blocks are created using mutually exclusive subsets of `profiles` within each block. This method produces a design with similar performance with that of the `"random"` method, except the choice sets are repeated and thus there will be many more opportunities for different respondents to see the same choice sets. For more information about blocking with full factorial designs, see `?DoE.base::fac.design` as well as the JSS article on the {DoE.base} package [@Gromping2018].

```{r}
design_full <- cbc_design(
  profiles = profiles,
  n_resp   = 900, # Number of respondents
  n_alts   = 3,   # Number of alternatives per question
  n_q      = 6,   # Number of questions per respondent
  method   = 'full'
)

dim(design_full) 
head(design_full)
```

## Orthogonal designs

The `"orthogonal"` method creates a design where an orthogonal array from the full set of `profiles` is found and then choice sets are created by randomly sampling from this orthogonal array *without replacement*. The choice sets are then repeated to meet the desired number of survey respondents (determined by `n_resp`). If blocking is used, choice set blocks are created using mutually exclusive subsets of the orthogonal array within each block. For cases where an orthogonal array cannot be found, a full factorial design is used. This approach is also sometimes called a "main effects" design since orthogonal arrays focus the information on the main effects at the expense of information about interaction effects. For more information about orthogonal designs, see `?DoE.base::oa.design` as well as the JSS article on the {DoE.base} package [@Gromping2018].

```{r}
#| message: true

design_orthogonal <- cbc_design(
  profiles = profiles,
  n_resp   = 900, # Number of respondents
  n_alts   = 3,   # Number of alternatives per question
  n_q      = 6,   # Number of questions per respondent
  method   = 'orthogonal'
)

dim(design_orthogonal) 
head(design_orthogonal)
```

## D-optimal designs

The `"dopt"` method creates a "D-optimal" design where an array from `profiles` is found that maximizes the D-efficiency of a linear model using the Federov algorithm, with the total number of unique choice sets determined by `n_q*n_blocks`. The optimization is handled using the [{AlgDesign} package](https://cran.r-project.org/package=AlgDesign). Choice sets are then created by randomly sampling from this array *without replacement*. The choice sets are then repeated to meet the desired number of survey respondents (determined by `n_resp`). If blocking is used, choice set blocks are created from the D-optimal array. For more information about the underlying algorithm for this method, see `?AlgDesign::optFederov` [@Wheeler2022].

```{r}
#| message: true

design_dopt <- cbc_design(
  profiles = profiles,
  n_resp   = 900, # Number of respondents
  n_alts   = 3,   # Number of alternatives per question
  n_q      = 6,   # Number of questions per respondent
  method   = 'dopt'
)

dim(design_dopt)
head(design_dopt)
```

## Bayesian D-efficient designs

The `"CEA"` and `"Modfed"` methods use the specified `priors` to create a Bayesian D-efficient design for the choice sets, with the total number of unique choice sets determined by `n_q*n_blocks`. The choice sets are then repeated to meet the desired number of survey respondents (determined by `n_resp`). These designs are optimized to minimize the D-error of the design given a prior model, which is handled using the [{idefix} package](https://CRAN.R-project.org/package=idefix). For now, designs are limited to multinomial logit priors (the {idefix} package can generate designs with mixed logit priors). These designs also currently do not support the ability to specify interaction terms in the prior model or use "labeled" designs. If `"CEA"` or `"Modfed"` is used without specifying `priors`, a prior of all `0`s will be used and a warning message stating this will be shown. In the opposite case, if `priors` are specified but neither Bayesian method is used, the `"CEA"` method will be used and a warning stating this will be shown. Restricted sets of `profiles` can only be used with `"Modfed"`. For more details on Bayesian D-efficient designs, see `?idefix::CEA` and `?idefix::Modfed` as well as the JSS article on the {idefix} package [@Traets2020].

In the example below, the prior model assumes the following parameters:

- 1 continuous parameter for `price`
- 2 categorical parameters for `type` (`'Gala'` and `'Honeycrisp'`)
- 2 categorical parameters for `freshness` (`"Average"` and `"Excellent"`)

```{r}
design_bayesian <- cbc_design(
  profiles  = profiles,
  n_resp    = 900, # Number of respondents
  n_alts    = 3, # Number of alternatives per question
  n_q       = 6, # Number of questions per respondent
  priors = list(
    price     = -0.1,
    type      = c(0.1, 0.2),
    freshness = c(0.1, 0.2)
  ),
  method = 'CEA'
)

dim(design_bayesian)
head(design_bayesian)
```

## Labeled designs (a.k.a. "alternative-specific" designs)

A "labeled" design (also known as "alternative-specific" design) is one where the levels of one attribute are used as a label. This can be created by setting the `label` argument to that attribute. As of now, only `"random"` and `"full"` methods support labeled designs. Since this by definition sets the number of alternatives in each question to the number of levels in the chosen attribute, the `n_alts` argument is overridden. Here is an example of a labeled random design using the `type` attribute as the label:

```{r}
design_random_labeled <- cbc_design(
  profiles = profiles,
  n_resp   = 900, # Number of respondents
  n_alts   = 3,   # Number of alternatives per question
  n_q      = 6,   # Number of questions per respondent
  label    = "type" # Set the "type" attribute as the label
)

dim(design_random_labeled)
head(design_random_labeled)
```

In the above example, the `type` attribute is now fixed to be the same order for every choice question, ensuring that each level in the `type` attribute will always be shown in each choice question.

## Designs with a "no choice" option (a.k.a. an "outside good")

A "no choice" (also known as an "outside good") option can be included by setting `no_choice = TRUE`. If included, all categorical attributes will be dummy-coded to appropriately dummy-code the "no choice" alternative. All design methods can have a "no choice" added.

```{r}
design_nochoice <- cbc_design(
  profiles  = profiles,
  n_resp    = 900, # Number of respondents
  n_alts    = 3, # Number of alternatives per question
  n_q       = 6, # Number of questions per respondent
  no_choice = TRUE
)

dim(design_nochoice)
head(design_nochoice)
```

For Bayesian D-efficient designs that include a "no choice" option, a prior for the "no choice" option must also be provided using `prior_no_choice`:

```{r}
design_bayesian_no_choice <- cbc_design(
  profiles  = profiles,
  n_resp    = 900, # Number of respondents
  n_alts    = 3, # Number of alternatives per question
  n_q       = 6, # Number of questions per respondent
  no_choice = TRUE,
  priors = list(
    price     = -0.1,
    type      = c(0.1, 0.2),
    freshness = c(0.1, 0.2)
  ),
  prior_no_choice = -0.1,
  method = 'CEA'
)

dim(design_bayesian_no_choice)
head(design_bayesian_no_choice)
```

# Inspect survey designs

The package includes some functions to quickly inspect some basic metrics of a design.

The `cbc_balance()` function prints out a summary of the individual and pairwise counts of each level of each attribute across all choice questions:

```{r}
design <- cbc_design(
  profiles = profiles,
  n_resp   = 900, 
  n_alts   = 3,   
  n_q      = 6
)

cbc_balance(design)
```

The `cbc_overlap()` function prints out a summary of the amount of "overlap" across attributes within the choice questions. For example, for each attribute, the count under `"1"` is the number of choice questions in which the same level was shown across all alternatives for that attribute (because there was only one level shown). Likewise, the count under `"2"` is the number of choice questions in which only two unique levels of that attribute were shown, and so on:

```{r}
cbc_overlap(design)
```

# Simulate choices

Choices for a given design can be simulated using the `cbc_choices()` function. This function requires a `design` argument (a design generated by `cbc_design()`), and an `obsID` argument, which is the column in `design` that identifies each unique choice observation. By default, random choices are simulated:

```{r}
data <- cbc_choices(
  design = design,
  obsID  = "obsID"
)

head(data)
```

Choices can also be simulated according to an assumed prior model. For this option, choices are simulated using the `predict.logitr()` method from the [{logitr} package](https://jhelvy.github.io/logitr/) [@Helveston2023], which makes predictions according to multinomial or mixed logit models.

The example below demonstrates how to simulate choices according to a multinomial logit model with fixed parameters. Note that for categorical variables (`type` and `freshness` in this example), the first level defined when using `cbc_profiles()` is set as the reference level. In this example, the parameters define the following utility model for each alternative _j_:

$$
u_{j} =
    -0.1 p_j +
    0.1 t^\mathrm{Gala}_j + 0.2 t^\mathrm{Honeycrisp}_j +
    0.1 f^\mathrm{Average}_j + 0.2 f^\mathrm{Excellent}_j +
    \varepsilon_{j}
$$

where $p$ is price, $t$ is type, and $f$ is freshness.

```{r}
#| eval: false

data <- cbc_choices(
  design = design,
  obsID = "obsID",
  priors = list(
    price     = -0.1,
    type      = c(0.1, 0.2),
    freshness = c(0.1, 0.2)
  )
)
```

The prior model used to simulate choices can also include interaction effects. For example, the example below is the same as the previous example but with an added interaction between `price` and `type`:

```{r}
#| eval: false

data <- cbc_choices(
  design = design,
  obsID = "obsID",
  priors = list(
    price = -0.1,
    type = c(0.1, 0.2),
    freshness = c(0.1, 0.2),
    `price*type` = c(0.1, 0.5)
  )
)
```

Finally, to simulate choices according to a mixed logit model where parameters follow a normal or log-normal distribution across the population, the `randN()` and `randLN()` functions can be used inside the `priors` list. The example below models the `type` attribute with two random normal parameters using a vector of means (`mean`) and standard deviations (`sd`) for each level of `type`:

```{r}
#| eval: false

data <- cbc_choices(
  design = design,
  obsID = "obsID",
  priors = list(
    price = -0.1,
    type = randN(mean = c(0.1, 0.2), sd = c(1, 2)),
    freshness = c(0.1, 0.2)
  )
)
```

# Assess power

The simulated choice data can be used to conduct a power analysis by estimating a model multiple times with incrementally increasing sample sizes. As the sample size increases, the estimated coefficient standard errors will decrease, enabling the experimenter to identify the sample size required to achieve a desired level of precision.

The `cbc_power()` function achieves this by partitioning the choice data into multiple sizes (defined by the `nbreaks` argument) and then estimating a user-defined choice model on each data subset. Model parameters are defined as a vector of attribute names that refer to column names in the `data` object. All models are estimated using the [{logitr} package](https://jhelvy.github.io/logitr/), and any additional arguments for estimating models with the \pkg{logitr} package can be passed through the `cbc_power()` function. For example, to assess power for a mixed logit model, the `randPars` argument can be used. For more information, see `?logitr::logitr` as well as the JSS article on the {logitr} package [@Helveston2023].

In the example below, the simulated choice data is broken into 10 chunks with increasing sample sizes and a multinomial logit model is estimated on each chunk with parameters for `price`, `type`, and `freshness`.

```{r}
power <- cbc_power(
  data    = data,
  pars    = c("price", "type", "freshness"),
  outcome = "choice",
  obsID   = "obsID",
  nbreaks = 10,
  n_q     = 6
)

head(power)
tail(power)
```

The returned data frame contains the coefficient estimates and standard errors for each chunk of the data. In the example above, it is clear that the standard errors for a sample size of 900 are much lower than those for a sample size of just 90. This approach can be used to more precisely identify sample size requirements by increasing `nbreaks`.

Visualizing the results of the power analysis can be particularly helpful for identifying sample size requirements. Since the `cbc_power()` function returns a data frame in a "tidy" (or "long") format [@Wickham2014], the results can be conveniently plotted using the popular {ggplot2} package [@Wickham2016]. A `plot.cbc_errors()` method is included in {cbcTools} to create a simple ggplot of the power curves.

```{r power}
plot(power)
```

Researchers may be interested in aspects other than standard errors. By setting `return_models = TRUE`, the `cbc_power()` function will return a list of estimated models (one for each data chunk), which can then be used to examine other model objects. The example below prints a summary of the last model in the list of returned models from a power analysis.

```{r}
models <- cbc_power(
  data    = data,
  pars    = c("price", "type", "freshness"),
  outcome = "choice",
  obsID   = "obsID",
  nbreaks = 10,
  n_q     = 6,
  return_models = TRUE
)

summary(models[[10]])
```

# Pipe it all together!

One of the convenient features of how the package is written is that the object generated in each step is used as the first argument to the function for the next step. Thus, just like in the overall program diagram, the functions can be piped together. For example, the "pipeline" below uses the Base R pipe operator (`|>`) to generate profiles, generate a design, simulate choices according to a prior utility model, conduct a power analysis, and then finally plot the results:

```{r}
#| eval: false

cbc_profiles(
  price     = seq(1, 4, 0.5), # $ per pound
  type      = c('Fuji', 'Gala', 'Honeycrisp'),
  freshness = c('Poor', 'Average', 'Excellent')
) |>
cbc_design(
  n_resp   = 900, # Number of respondents
  n_alts   = 3,   # Number of alternatives per question
  n_q      = 6    # Number of questions per respondent
) |>
cbc_choices(
  obsID = "obsID",
  priors = list(
    price     = -0.1,
    type      = c(0.1, 0.2),
    freshness = c(0.1, 0.2)
  )
) |>
cbc_power(
    pars    = c("price", "type", "freshness"),
    outcome = "choice",
    obsID   = "obsID",
    nbreaks = 10,
    n_q     = 6
) |>
plot()
```

```{r, ref.label='power', echo=FALSE}
```

## Comparing multiple designs

When evaluating multiple designs, it can be helpful to visually compare their respective power curves. This can be done using the `plot_compare_power()` function. To use it, you have to first create different designs and then simulate the power of each design by simulating choices. Here is an example comparing a full factorial design against a Bayesian D-efficient design:

```{r}
# Make designs to compare: full factorial vs bayesian d-efficient
design_full <- cbc_design(
  profiles = profiles,
  n_resp = 300, n_alts = 3, n_q = 6
)
# Same priors will be used in bayesian design and simulated choices 
priors <- list( 
  price     = -0.1,
  type      = c(0.1, 0.2),
  freshness = c(0.1, 0.2)
)
design_bayesian <- cbc_design(
  profiles  = profiles,
  n_resp = 300, n_alts = 3, n_q = 6, n_start = 1, method = "CEA",
  priors = priors, parallel = FALSE
)

# Obtain power for each design by simulating choices
power_full <- design_full |>
cbc_choices(obsID = "obsID", priors = priors) |>
  cbc_power(
    pars = c("price", "type", "freshness"),
    outcome = "choice", obsID = "obsID", nbreaks = 10, n_q = 6, n_cores = 2
  )
power_bayesian <- design_bayesian |>
  cbc_choices(obsID = "obsID", priors = priors) |>
  cbc_power(
    pars = c("price", "type", "freshness"),
    outcome = "choice", obsID = "obsID", nbreaks = 10, n_q = 6, n_cores = 2
  )

# Compare power of each design
plot_compare_power(power_bayesian, power_full)
```

# References